Solving Recurrences - Substitution method
Methods to solve the recurrences to get bounds on the runtime are :1. Substitution method
2. Recursion tree
3. Master theorem
1. Substitution method
The substitution method for solving recurrences
comprises two steps:
1. Guess the form of the solution.
2. Use mathematical induction to find the constants and show
that the solution works.
Example: Recurrence:
We guess that the solution is T(n) = O(n log n). So we must
prove that T(n) <= c n log n for some constant c.
As our inductive
hypothesis, we assume T(n) = c n log n for all positive numbers less than n.
and
Now we need to show the base case. This is tricky, because if
T(n) ≤ cn log n, then T(1) ≤ 0,
which is not a thing( T(1) = 1 given)
So revise our induction so
that we only prove the statement for n ≥2, and the base cases of the induction
proof are n = 2 and n = 3.
n = 2 and n = 3 is choose as
base cases because when the recurrence formula is expanded , we will always go
through either n = 2 or n = 3 before we hit the case where n = 1.
Plugging the numbers into the recurrence formula, we get
T(2)
= 2T(1) + 2 = 4 and
T(3) = 2T(1) + 3 = 5.
So now we just need to choose a c that satisfies those
constraints on T(2) and T(3).
We can choose c = 2, because 4 ≤ 2 .2 log 2
and 5 ≤2 .3 log 3.
Therefore, we have shown that T(n) ≤ 2n log n for all n ≥ 2,
so T(n) = O(n log n).
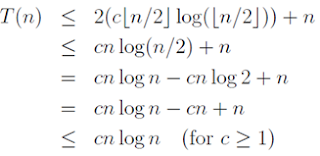
No comments:
Post a Comment