Solving Recurrences - Recursion Tree method
Methods to solve the recurrences to get bounds on the runtime are :1. Substitution method
2. Recursion tree
3. Master theorem
2. The recursion-tree method for solving recurrences
A recursion tree is a tree where each node
represents the cost of a certain recursive sub-problem.
Then you can sum up the numbers in each
node to get the cost of the entire algorithm.
A recursion tree is best used to generate a good guess, which
you can then verify by the substitution method.
Example:
Consider a recurrence:
Drop
the floors and write a recursion tree for T(n) = 3T(n /4) + cn2.
For convenience, assume that n is an exact power
of 4 so that all subproblem sizes are integers.
Part (a) of the figure shows T(n), which we
expand in Part (b) into an equivalent tree representing the recurrence. The cn2
term at the root represents the cost at the top level of recursion, and the
three subtrees of the root represent the costs incurred by the subproblems of
size n/4.
Part
(c) shows this process carried one step further by expanding each node with
cost T(n/4) from Part (b). The cost for each of the three children of the root
is c(n/4)2.
Because
subproblem sizes decrease by a factor of 4 each time we go down one level, we
eventually must reach a boundary condition.
The
subproblem size for a node at depth i is n=4i. Thus, the subproblem
size hits n =1 when n / 4i = 1 or, equivalently, when i = log4
n. Thus, the tree has log4 n +1 levels (at depths
0,1,2,.........,log4 n).
Next
we determine the cost at each level of the tree. Each level has three times
more nodes than the level above, and so the number of nodes at depth i is 3i. And because
subproblem size reduce by a factor of 4 for each level we go down from the
root, each node at depth i, for i = 0,1,2,…….,log4 n-1, has a cost
of c(n/4i )2.
Therefore the
total cost over all nodes at depth i, for i = 0,1,2,…..,log4 n -1,
is
3i
c(n/4i )2 = (3 /16)i c n2.
The
bottom level, at depth log4 n, has 3log4
n = nlog4 3 nodes, each contributing
cost T(1) for a total cost of nlog4 3T(1),
which is θ(nlog4 3), since we assume that T(1)
is a constant.
Now
we add up the costs over all levels to determine the cost for the entire tree:
Can be written as,
Thus,
we have derived a guess of T (n) = O(n2) .
Now use the substitution method to verify the guess correctness.
We
want to show that T (n) ≤ dn2 for some constant d > 0.
Using
the same constant c > 0 as before, we have
where the last step holds as long as d ≥ (16/3)c.(when c
=(3/16)d, i.e. d ≥ (16/3)c).
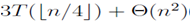



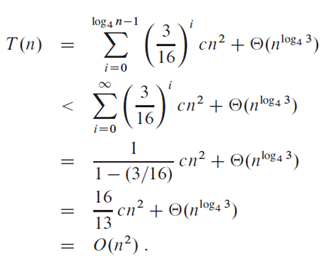

No comments:
Post a Comment