Rod-cutting problem

Rod-cutting problem 

The rod-cutting problem is the following. Given a rod of length n inches and a table of prices p_i for i = 1, 2,……,n, determine the maximum revenue r_n obtainable by cutting up the rod and selling the pieces.

 

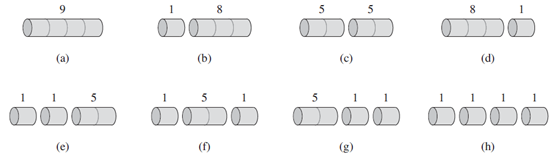
Consider a rod of length 4 inches is given ( n=4).

A rod of length n can be cut up in 2^n-1 different ways. For a rod of length 4, there are eight different ways to cut it.

The best strategy is cutting it into two pieces of length 2, which gives you 10 rupees. Two 2-inch pieces produces revenue p_{2 +}p₂ = 5+5 = 10, which is optimal.

Let r_i be the maximum amount of money you can get with a rod of size i. The problem can be viewed recursively as follows:

1.      First, cut a piece off the left end of the rod, and sell it.

2.      Then, find the optimal way to cut the remainder of the rod.

Trying all possible cases, first try cutting a piece of length 1, and combining it with the optimal way to cut a rod of length n-1. Then try cutting a piece of length n-2, and combining it with the optimal way to cut a rod of length n-2. Try all the possible lengths and then pick the best one. This end up with

This formula immediately translates into a recursive algorithm.

Procedure CUT-ROD takes as input an array p[1.. n] of prices and an integer n, and it returns the maximum revenue possible for a rod of length n.

The recursion tree showing recursive calls resulting from a call CUT-ROD(p.n) for n = 4.

A path from the root to a leaf corresponds to one of the 2^n-1 ways of cutting up a rod of length n. In general, this recursion tree has 2ⁿ nodes and 2^n-1 leaves. 

Thus, T (0) = 1     and 

 The running time of CUT-ROD is exponential in n , T (n) = 2ⁿ

Using dynamic programming for optimal rod cutting

A naive recursive solution is inefficient because it solves the same sub problems repeatedly. Using Dynamic programming each sub problem is solved only once, saving its solution. If solution to this sub problem is required again later, just look it up, rather than recompute it.

Dynamic programming thus uses additional memory to save computation time; an exponential-time solution may be transformed into a polynomial-time solution.

A dynamic-programming approach runs in polynomial time when the number of distinct sub problems involved is polynomial in the input size and each such sub problem can be solved in polynomial time.

There are usually two equivalent ways to implement a dynamic-programming approach.

The first approach is top-down with memorization. In this approach, we write the procedure recursively in a natural manner, but modified to save the result of each sub problem (usually in an array or hash table). The procedure now first checks to see whether it has previously solved this sub problem. If so, it returns the saved value, saving further computation at this level; if not, the procedure computes the value in the usual manner. 

The second approach is the bottom-up method. This approach typically depends on some natural notion of the “size” of a sub problem, such that solving any particular sub problem depends only on solving “smaller” sub problems. Sort the sub problems by size and solve them in size order, smallest first. When solving a particular sub problem, already the smaller sub problems are solved for its solution, and saved their solutions. 

These two approaches yield algorithms with the same asymptotic running time, except in unusual circumstances where the top-down approach does not actually recurse to examine all possible sub problems.

Memoization (top down approach) rod cutting problem

Run time: θ (n²). Each sub problem is solved exactly once, and to solve a sub problem of size i, we run through i iterations of the for loop. So the total number of iterations of the for loop, over all recursive calls, forms an arithmetic series, which produces θ (n²) iterations in total.

Bottom up approach

Run time: θ(n²), because of the double for loop. The bottom-up and top-down versions have the same asymptotic running time.

Dynamic-programming solutions to the rod-cutting problem returns the value of an optimal solution, but they do not return an actual solution: a list of piece sizes. 

Extending the dynamic-programming approach to record not only the optimal value computed for each sub problem, but also a choice that led to the optimal value is

The following procedure takes a price table p and a rod size n, and it calls EXTENDED-BOTTOM-UP-CUT-ROD to compute the array s[1 . . n] of optimal first-piece sizes and then prints out the complete list of piece sizes in an optimal decomposition of a rod of length n: