A Graph is a non-linear data
structure consisting of nodes and edges. The nodes are sometimes also referred
to as vertices and the edges are lines or arcs that connect any two nodes in
the graph.
A Graph consists of a
finite set of vertices(or nodes) and set of Edges which connect a pair of
nodes.
Two most commonly used
representations of a graph.
1. Adjacency Matrix
2. Adjacency List
2. Adjacency List
The choice of the graph
representation is situation specific. It totally depends on the type of
operations to be performed and ease of use.
Adjacency Matrix:
Adjacency Matrix is a two dimension
array of size V x V where V is the number of vertices in a graph. Let the 2D
array be adj[ ][ ], a slot adj[i][j] = 1 indicates that there is an edge from
vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric.
Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w,
then there is an edge from vertex i to vertex j with weight w.
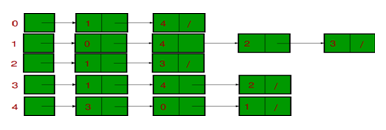
Adjacency List:
An array of lists is used. Size of
the array is equal to the number of vertices. Let the array be array[]. An
entry array[i] represents the list of vertices adjacent to the ith
vertex. This representation can also be used to represent a weighted graph. The
weights of edges can be represented as lists of pairs.
Following is adjacency
list representation of the above graph.


No comments:
Post a Comment