Minimum Spanning Tree (MST)

Minimum Spanning Tree (MST)

Given a connected and undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees.

A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree. The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

Following are a few properties of the spanning tree connected to graph G −

• A connected graph G can have more than one spanning tree.
• All possible spanning trees of graph G, have the same number of edges and vertices.
• The spanning tree does not have any cycle (loops).
• Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.
• Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.

Mathematical Properties of Spanning Tree

• Spanning tree has n-1 edges, where n is the number of nodes (vertices).
• From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.
• A complete graph can have maximum n^n-2 number of spanning trees.

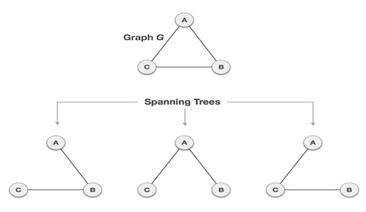
A complete undirected graph can have maximum n^n-2 number of spanning trees, where n is the number of nodes. In the below given example, n is 3, hence 3³⁻² = 3spanning trees are possible.

A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.

Two most important spanning tree algorithms here −

• Kruskal's Algorithm
• Prim's Algorithm