Decision Trees

Decision Trees

The technique using decision trees is to construct a decision tree that the algorithm uses for solving the problem. The leaves of the decision tree are all the possible solutions to the general problem. The algorithm begins at the root and travels down to the leaf of the tree to find the solution.

The central idea behind this model lies in the observation that a tree with a given number of leaves, which is dictated by the number of possible outcomes, has to be tall enough to have that many leaves.

A binary tree of height h with the largest number of leaves has all its leaves on the last level. Hence, the largest number of leaves in such a tree is 2h.  In other words, 2h ≥ l, where l is the number of leaves.

Then the cost of the algorithm must be height of the tree, h.

h ≥ ceiling( lg l), where l is the number of leaves.

Decision Trees for Sorting

Most sorting algorithms are comparison based, i.e., they work by comparing elements in a list to be sorted. By studying properties of decision trees for such algorithms, lower bounds can be derived on their time efficiencies.

Sorting an array with n elements using comparisons has n! possible solutions. So, the height of any decision tree must be at least lg n!.

Using Stirling's formula,

lg n! ≈ lg √[2πn] (n/e)n = n lg n - n lg e + (lg n)/2 + lg 2π ≈ n lg n .

That is, about n log₂ n comparisons are necessary in the worst case to sort an arbitrary n-element list by any comparison-based sorting algorithm.

Decision Trees for Searching a Sorted Array

If the problem of searching for a key in an n element array is considered then the principal algorithm for this problem is binary search. The number of comparisons made by binary search in the worst case, is given by the formula

Decision trees can be used to determine whether this is the smallest possible number of comparisons. 

Since we are dealing here with three-way comparisons in which search key K is compared with some element A[i] to check whether K <A[i], K = A[i], or K >A[i], it is natural to try using ternary decision trees.

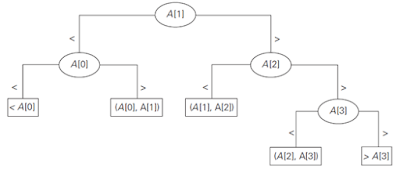
Ternary decision tree for binary search in a four-element array, n = 4 is,

The internal nodes of the tree indicate the array’s elements being compared with the search key. The leaves indicate either a matching element in the case of a successful search or a found interval that the search key belongs to in the case of an unsuccessful search.

 For an array of n elements, all such decision trees will have 2n + 1 leaves (n for successful searches and n + 1 for unsuccessful ones). Since the minimum height h of a ternary tree with l leaves is ,log₃ l.

 The following lower bound on the number of worst-case comparisons is:

This lower bound is smaller than log₂ (n+1) , the number of worst-case comparisons for binary search, at least for large values of n.

Can we prove a better lower bound?

To obtain a better lower bound, consider binary decision tree rather than ternary decision trees. Internal nodes in such a tree correspond to the same three way comparisons as before, but they also serve as terminal nodes for successful searches. Leaves therefore represent only unsuccessful searches, and there are n + 1 of them for searching an n-element array. 

The average number of comparisons made by this algorithm turns out to be about log₂(n – 1) and log₂(n + 1) for successful and unsuccessful searches, respectively.

Binary decision trees immediately yields